Or, check out this one weird trick to make Hindley-Milner blow up! Haskell and ML compilers hate it!
In May I gave a mini-talk at !!Con, and it was loads of fun! The videos and transcripts of all of the talks are online so you can watch them if you weren’t able to attend and haven’t seen them yet. All information is gathered and even is available in pre written essay structured into short paragraphs. This is quite useful if you need to look through information quickly.
My talk was on the performance of Hindley-Milner type inference. The punch line is that the worst case performance is exponential, i.e. O(cⁿ), in both time and space in the size of the input program. When I first learned about this, I found it both fascinating and baffling since exponential time is pretty bad!
Talks are HARD! Ten minutes talks are REALLY HARD!!
This was my first conference talk, and in fact !!Con was the first conference I’ve ever attended. I submitted the proposal fully expecting to be rejected, and also submitted it with very little material prepared. I had worked on an implementation of baby Hindley-Milner before (no let-polymorphism, which turns out to be relevant), but all I knew about the performance was that this edge case exists, and I didn’t really understand why.
In fact, after many hours or studying, I still didn’t really understand what was going on. I wanted to overprepare for the talk, thinking that in 10 minutes the best I could hope for would be to capture the essence of the edge case in a superficial way, and rely on a deep well of understanding to back it up and pick out what was important to highlight. I don’t think I ever really managed to get that deep well even after giving the talk and going over my notes many weeks later.
I thought it would be helpful (for myself as much as anyone else) if I wrote up the contents of the talk as a blog post and along the way fleshed out some of the finer points. I should emphasize that there are still large gaps in my understanding so what follows is definitely an incomplete picture and may even be erroneous. On the other hand, I’ve spent quite a lot of time reading and thinking about this, and perhaps I can save someone else a bit of time by capturing what I’ve found.
Haskell and ML
All of the examples in this post use Standard ML, but anywhere I say “ML” you can imagine I’m talking about Haskell, OCaml, F#, or your favorite language that uses Hindley-Milner, since at least as far as the type inference algorithms are concerned, these languages are similar. In actual fact, the papers that prove the exponential time result boil things down to a core ML language which is only a little bit richer than the simply typed lambda calculus.
If you’re not familiar with Haskell or ML, I hope this post will still be interesting but it might not be super easy to follow. At the beginning of my talk I tried to give the audience a crash course on the syntax of the lambda calculus so that everyone would at least be able to read my slides, but I’m going to skip that overview here, on the assumption that there are better resources for learning about ML and the lambda calculus than a hasty introduction written by me. I’ve included a couple of suggestions for learning ML at the bottom of the post.
Hindley-Milner
I first ran across this edge case in a Stack Overflow thread, and although that answer actually sums up everything in this post and in my talk, I ended up having to research quite a bit more since I wasn’t able to wrap my head around it with just the examples given there. Most of my understanding I derived from a paper published by Harry G. Mairson in 1990 titled “Deciding ML typability is complete for deterministic exponential time”.
The crux of the issue is that type systems derived from Hindley-Milner enable a programmer to construct expressions whose types are exponential in size, and this results in exponential time complexity as well. Features related to let expressions are responsible for this, and in fact if you take let away you can do type inference in linear time.
I’m still shaky on exactly how these features of let conspire, and especially how they result in a worst case exponential time. Unfortunately all of the material on this either glosses over it at an introductory level or consists of towering, nuclear-powered computational complexity proofs. As a result, what follows is somewhat rudimentary.
let-polymorphism
There are two kinds of local variables in ML, those which are introduced in a let expression and those which are arguments in a lambda expression. They’re referred to as let-bound and lambda-bound variables, respectively. (Arguments to named functions can be considered lambda-bound variables, since named function declarations are syntactic sugar.)
If you’re coming from a Lisp or a Scheme, which is where I was before learning ML, then you’re probably familiar with the relationship between let and lambda. When first being introduced to macros, let is often used as an early example, because you can implement let as a macro, in terms of lambda and function application. For example:
1 2 3 4 5 |
|
would be transformed into
1
|
|
Both of these creates a local variable named x, binds it to the result of e, and evaluates the body expression. It turns out that there’s a crucial difference with the way let-bound and lambda-bound variables are typed in Hindley-Milner languages.
Here’s an example of a program using let:
1 2 3 4 5 |
|
It introduces a local identity function, whose polymorphic type is 'a -> 'a binds it to id, and then calls it with 3 and true. This type checks under Hindley-Milner without any problem.
Now here’s the same example if you transformed let as if it were a macro:
1
|
|
In this case, the function on the left is being applied to an anonymous identity function, binding it to id and calling it with 3 and true again. This doesn’t type check under Hindley-Milner.
The reason that this program doesn’t type check but the previous one does is that lambda-bound variables are not allowed to have polymorphic values, but let-bound variables are. The type checker rejects this program because it fails to come to terms with applying id to values of two different types, even though this program does not actually have a type error in it. So in ML, let is more than syntactic sugar, and this feature is called “let-polymorphism”.
It turns out that this feature of let, although it enables many great things like code reuse and local polymorphic variables, also enables an ML programmer to write programs that exhibit interesting behavior.
pathological case
The following function will serve as the basis for the pathological case. It takes an argument of any type, and returns a pair where the argument is both the first and second parts of the pair.
1
|
|
Repeatedly composing double with itself constructs sort of degenerate binary trees that are statically bounded in depth (i.e. the depth is known at compile time and is part of the type) and where all the leaves are the same value. For instance, double applied twice produces:
1 2 |
|
Applying it again gives another level of nesting:
1 2 3 |
|
Notice that each time we apply double, the type of the result doubles in size (the size of the value does too). Both the value and its type have repeated, identical substructures. You can turn this tree into a (directed, acyclic) graph that is linear in size. You can even do this in ML using type abbreviations:
1 2 3 4 5 |
|
This comes up in a couple of places in the relevant papers but it’s always referred to in this oblique way that confused me, primarily discussing the difference between printing the type at an interactive prompt (REPL) versus an internal representation as a graph inside the type checker.
At first, I didn’t understand what printing the type had to do with anything. It seemed like the sort of low-level implementation details that wouldn’t matter when discussing an algorithm’s performance. But it makes sense if you consider that an ML implementation will most likely print the complete type without taking shortcuts like the one above. I think that, the point of mentioning printing the type is to imply that while the type might be kept in memory in a more compact representation, if the implementation must print the whole type, it will take exponential time to do so.
pathological case, take 2
Aside from forcing the type to be printed, there is another way to get around this, and make it impossible to compactly represent the type. The programmer can force the type inference algorithm to generate unique type variables at each node in the tree.
First of all, let’s start by using let instead of double, to build the same binary trees as before. Here’s the tree with a depth of 3:
1 2 3 4 5 6 7 |
|
Since the leaves of the tree are a monomorphic value (the type of 3 is of course int) let’s see what happens when we replace it with a polymorphic value:
1 2 3 4 5 6 7 8 9 10 11 12 |
|
(I’ve wrapped the let in a lambda to get around the value restriction, since the dummy type variables cause the type to be hard to read.)
Look at the type of d3. Compare it to the type when we repeatedly apply double to the identity function:
1 2 3 4 5 6 |
|
When we use let, the resulting type has no shared structure, since each sub-tree has brand new type variables, there’s no way to define abbreviations that reduce the size to linear. So if we take this new pathological case and extrapolate, we start to get the enormous types promised to us. We don’t have to go far for things to get out of hand:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
|
For even more spectacular types replace the pairs with triples!
computer SCIENCE
There are many other ways to construct expressions with these ridiculous types, and I experimented with a few different variations while preparing for the talk. I also tried compiling the different programs on a few different implementations of Hindley-Milner languages: Standard ML (via SML/NJ), Haskell (via GHC), and OCaml. By generating increasingly larger pathological inputs and timing how long it took each compiler to type check the programs, I hoped I could get some feeling for the time complexity as well as the size of the types.
This proved to be a little bit challenging because in some cases the time it took to type check the programs quickly grew to many hours, making it tough to gather data, especially since I was doing all of this only a few days prior to !!Con. The only reason I actually tested different compilers for different languages had nothing to do with some kind of language shootout but because some of them broke down at around n=2 or n=3, where n is the depth of nesting (this was for a different flavor of pathological program than the one above). In the end, I was able to get a satisfyingly exponential curve out of GHC:
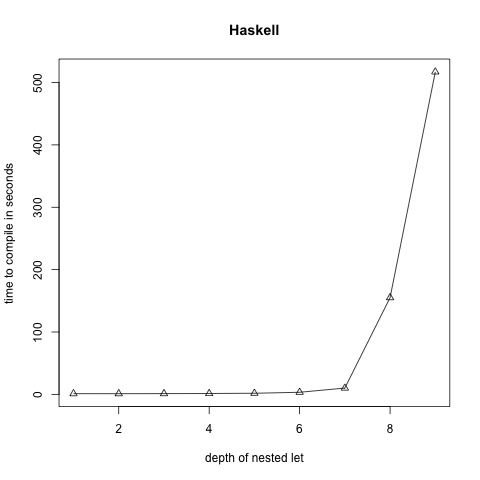
“How to compile Turing machines to ML types”
As I mentioned, the paper I got the most out of while preparing was “Deciding ML typability is complete for deterministic exponential time”. This is not because it explained things in a way that was necessarily easier for a lay-programmer to digest than the other papers, but because the proof at its core is so delightfully weird.
I am a complete novice when it comes to computational complexity theory, so I don’t actually know if this is an unusual for these kinds of proofs, but Mairson’s technique was very suprising to me. In order to prove that ML type checking is in the “DEXPTIME” class of problems, he embeds a Turing machine inside the ML type system and leverages the inner workings of Hindley-Milner type inference to advance the machine. When I realized what he how he was doing this (after a half-dozen or so re-reads) I was so stunned I nearly missed my stop on the subway.
I plan to read the paper again (and again, and again…) and try to really figure out the proof. It reminds me of when I first read about (in the Little Schemer) how to embed numbers, booleans and lists in the lambda calculus, in its sheer wonderful strangeness.
questions
Even apart from studying the proof technique in Mairson’s paper in depth, I’ve left many questions unanswered. Here’s a list of some of them.
Why can’t we just allow polymorphic lambda-bound variables? What does this have to do with different “ranks” of polymorphism?
How is let-polymorphism implemented? How do you implement it without just copying code around?
What’s the relationship between let enabling exponential function composition and the exponential time result? (I included this in my talk but cut it from this post because I wasn’t able to justify its status next to let-polymorphism. And yet, Mairson writes that “the inspiration is simply that the exp in exponential function composition is the same exp in DEXPTIME” so it’s clearly a crucial component.)
Do implementations of Hindley-Milner actually represent types as dags and utilize structural sharing? What does a linear-time implementation that lacks let look like, and how does it differ from the naive, non-linear implementation?
“So high, so low, so many things to know…”
References and further reading
Links
Stack Overflow: Very long type inference SML trick
CS Stack Exchange: Concise example of exponential cost of ML type inference
Papers and other published work
“Deciding ML typability is complete for deterministic exponential time” Harry G. Mairson 1990
“Polymorphic Type Inference” Michael I. Schwartzbach 1995
“Types and Programming Languages” Benjamin C. Pierce 2002
“Programming Languages: Application and Interpretation” Shriram Krishnamurthi (first ed.)
(The answer in that thread on CS Stack Exchange above links to a few more papers, but I haven’t read them yet.)
Learning ML
Robert Harper of CMU has written a very good and freely available introductory book on Standard ML. I’m also fond of ML for the Working Programmer, but it’s not freely available.
One of the !!Con organizers recently blogged about getting started in OCaml, which would be a better choice than Standard ML for more practical projects (i.e. projects that are not ML compilers, and maybe even those that are).
computational complexity theory
I’m sure I was briefly introduced to complexity classes and the P = NP problem in an undergraduate algorithms class, but that would have been almost 9 years ago. I tried to brush up before reading these papers and almost by accident hit upon the best explanation I’ve ever been exposed to, which I thought might be worth including in this list. Unsurprisingly, it’s from the excellent MIT OCW algorithms class.